Noether normalization lemma

In mathematics, the Noether normalization lemma is a result of commutative algebra, introduced in (Noether 1926). A simple version states that for any field k, and any finitely generated commutative k-algebra A, there exists a nonnegative integer d and algebraically independent elements y1, y2, ..., yd in A such that A is a finitely generated module over, and hence also an integral extension of, the polynomial ring B:=k[y1, y2, ..., yd].

The integer d is uniquely determined by A: it is the Krull dimension of A. When A is an integral domain, d is then the transcendence degree of the field of fractions of A over k.

The lemma can be understood geometrically. Suppose A is integral. Let B be the coordinate ring of d-dimensional affine space 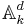\mathbb A^d_k, and A as the coordinate ring of some other d-dimensional affine variety X. Then the inclusion map B → A induces a surjective finite morphism of affine varieties 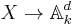X\to \mathbb A^d_k. The conclusion is that any affine variety is a branched covering of affine space. When k is infinite, such a branched covering map can be constructed by taking a general projection from an affine space containing X to a d-dimensional subspace.

The form of the Noether normalization lemma stated above can be used as an important step in proving Hilbert's Nullstellensatz. This gives it further geometric importance, at least formally, as the Nullstellensatz underlies the development of much of classical algebraic geometry.

References